Funciones trigonometricas de un angulo en posicion normal

  SIGNOS DE LAS FUNCIONES TRIGONOMÉTRICAS DE UN ANGULO EN                                                                        POSICIÓN NORMAL
Para determinar el signo de las funciones trigonométricas se deben analizar el comportamiento de R, X, Y.
Si Ө es un angulo es posición normal y P (x,y) es un punto sobre el lado final de Ө diferente de 0 (0,0)


Resultado de imagen para signos de las funciones trigonometricas de un angulo en posicion normal 

0P = r = √^2 + y^2




.X yY varían dependiendo el variante en que se encuentre por lo tanto el signo de los valores trigonométricas para cada angulo depende de los signos X,Y. En el siguiente cuadro se presentan los signos de las funciones  del angulo Ө en posición normal para los diferentes cuadrantes en que puede estar ubicado el lado final.



Resultado de imagen para cuadro de variable trigonometrica funcion cuadrante


EJEMPLO:

Si tanӨ es =  -2/1
y el lado final de Ө esta en el tercer cuadrante determina el valor de senӨ y cosӨ
tanӨ  = 2/1 = y/x = -2 /-1

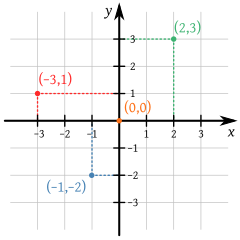
Imagen relacionada 

r = √x^2 + y^2

r = √(-1)^2 + (-2)^2 = √ 1 + 4 = √5

SenӨ = -1/√5            CosӨ = -2/√5

                       FUNCIONES TRIGONOMÉTRICAS DE LAS ∡ CUADRANTES 


.Hasta el momento se ha estudiado los ángulos cuyo lado final se encuentran  en una de las 4 cuadrantes , ahora es importante considerar los ángulos cuyo lado final coincide con uno de los semi eje del plano cartesiano se le llama ángulos cuadrantes, en la siguiente figura se muestra los ángulos cuadrantes 90º, 180º, 540º , -90º y -180º.





Para determinar las funciones trigonométricas de los cuadrantes, se considera que sobre su lado final se encuentren algunos de los puntos (o,r) , (-r,o) , (o,-r), (r,o) ＞O



En el siguiente cuadro se presenta los valores de las funciones para los ángulos cuadrantes mayores o iguales que (0) o menores o iguales a (0)


Resultado de imagen para cuadro de las funciones trigonometricas de los angulos cuadrantes



EJEMPLO:

1. Si Ө es un angulo en posición normal cuyos lados terminales están en el cuadrante dado, encontrar los valores exactos de las otras 6 funciones trigonométricas de Ө, si están determinadas por:

⋕Cos Ө = -1/2 Ⅱ

Solución:

⋕Cos Ө = -1/2 = r^2 = X^2 + Y^2
 
                            2^2 = 1^2  + Y^2
   
                                4 = 1 + Y^2

                            Y^2 = 4 - 1 = 5

                            Y^2 = 3

                            Y = 土 √3
SenӨ = √3/2

TanӨ = √3/1

CotӨ = 1/√3

SecӨ = 2/1

CscӨ = 2/√3



⋕Sen 7ㅠ/2 = (-1)  Tan 720º = 0

R\= 7ㅠ/2  x 180/ㅠ = 1260/2 = 630

Comentarios

Publicar un comentario

Entradas más populares de este blog

Razones trigonométricas en un triangulo rectángulo

Imagen
 RAZONES TRIGONOMÉTRICAS EN UN TRIANGULO RECTÁNGULO Senθ = y/r = cateto opuesto/hipotenusa Cosθ = x/r = cateto adyacente/hipotenusa Tanθ = y/x = cateto opuesto/cateto adyacente Cotθ = x/y = cateto adyacente/cateto opuesto Secθ = r/x = hipotenusa/cateto adyacente Cscθ = r/y = hipotenusa/cateto opuesto CONOCE: Los triángulos rectángulos ABC y EBD son semejantes porque cumplen  el criterio de semejanza angulo-angulo. Los dos tienen un angulo recto y comparten la medida del angulo de 33, 69º. por lo tanto, el angulo de es congruente con el angulo  C; es decir de = 56, 31º Por ser triangulo  semejantes, se pueden establecer razones y proporciones entre los medidas de sus lados y así hallar la medida del segmento AB AC/ED = AB/EB , entonces 4/2 = AB/3 Por lo tanto; AB = b Otro tipo de razones se pueden establecer entre las medidas de los lados  y los ángulos agudos en un triangulo  rectángulo. Estas razones se denominan razon...
Leer más

Circunferencia unitaria

Imagen
                                           CIRCUNFERENCIA UNITARIA . El estudio de las funciones trigonométricas requieren el análisis de sus comportamientos  y de la identificación de su dominio y su rango. Para realizar dicho análisis se considera la circunferencia de radio uno centrada en el plano cartesiano. La circunferencia unitaria es aquella que tiene como centro el origen del plano cartesiano y de radio la unidad. En la figura anterior se muestra la circunferencia unitaria que contiene al punto P(x,y). Al aplicar el teorema de pitagoras se obtiene que para cada punto P(x,y) se cumple que  x^2 + y^2 = 1 .Si θ es un angulo en posición normal cuya medida es igual Trad la medida del arco S subtendido por dicho angulo en la circunferencia unitaria se obtiene mediante.. Ejemplo . Verificar que el punto M (1/2 - √3/2) pertenece a la circunferencia uni...
Leer más